Standard Roof Pitch to Degrees • Roof Angle in Degrees to Roof Pitch

Slope Conversion Charts • Slope Conversion Formulas

By Jack Gray, Roof Online Editor • Updated October 13, 2022

See More Roofing Topics

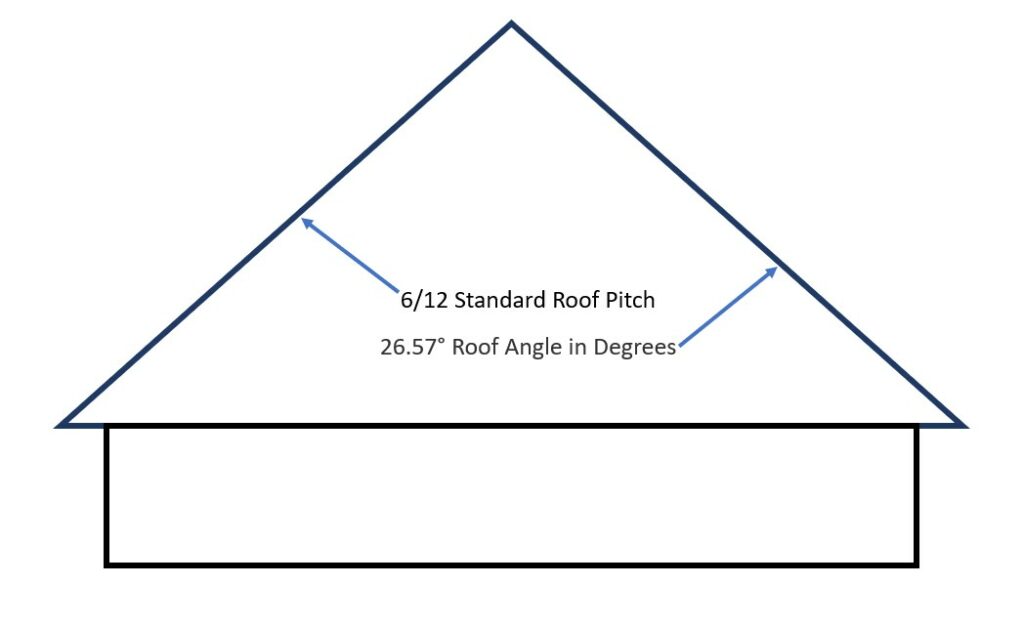
Table of Contents

• Why Convert Roof Pitch to Degrees or Vice Versa?
• Note: Correct Format When Stating Roof Pitch
• Useful Roof Slope Tools
• How to Convert Standard Roof Pitch to Degrees
  • About This Roof Pitch to Degrees Conversion Table
  • Conversion Formula for Standard Roof Pitch to Degrees
  • Table 1: Standard Roof Pitch to Degrees Conversion
• How to Convert Roof Angle in Degrees to Standard Roof Pitch
  • About This Degrees to Roof Pitch Conversion Table
  • Conversion Formula for Degrees to Standard Roof Pitch
  • Table 2: Slopes in Degrees Converted to Standard Roof Pitch
• Related Pages

Why Convert Roof Pitch to Degrees or Vice Versa?

There are a few reasons why you’d want to convert roof pitch to degrees or convert a roof slope in degrees to standard roof pitch. But the main issue that comes to mind is the fact that technical literature relating to specific roofing products or roof design more generally often use one or the other, but not both.

This is definitely a problem for English-speaking people outside of the United States reading American roofing literature, and vice versa. Say you’re used to standard roof pitch, you’re checking out a new roofing product on a foreign company’s website, and you read that the product has a minimum slope requirement of 20°. It can slow you down.

A good roof pitch to degrees chart would be a nice to have. Being able to quickly convert standard roof pitch to degrees comes in handy in those situations, and that’s the main reason we put these tables together.

Note: Correct Format When Stating Roof Pitch

When discussing roof pitch, the proper way to state a specific pitch is in the form “X-in-12”, so if you’re talking about a roof that rises 6 units for every 12 units it runs horizontally, you would say that the roof has a 6 in 12 pitch.

In roofing industry literature, the standard abbreviation used for indicating a particular roof pitch has a colon and takes the form “X:12” or “X : 12”, so for a 6 in 12 pitch, you would write “6:12 pitch”.

As a practical matter, an overwhelming number of people looking for information about roof pitch on the internet search for a roof pitch using a slash, as in “6/12”. In order to help more people find what they’re looking for, we are using the “X/12” form in our first table below.

Useful Roof Slope Tools

If you’re not sure what the slope of your roof is and you want to determine that in either degrees or standard roof pitch, we recommend this slope finder on Amazon. It’s very inexpensive and very accurate.

If you want to know the slope of anything to an amazing degree of accuracy and you like cool new tools, you should check out this digital level.

It may be way too expensive for what you need, but this is what professionals use. It will tell you the slope of your roof in degrees, rise/run, or percentage, and automatically convert from one to the other. In other words, it will do everything this article explains how to do.

If you’re using this table, you may want to look into getting yourself a construction calculator. This one is very good.

How to Convert Standard Roof Pitch to Degrees

About This Roof Pitch to Degrees Conversion Table

The following table shows the degree equivalents for all roof slopes in standard pitch from ⅛-in-12 to 36½-in-12.

To see the percentage equivalents for standard rise-in-run roof pitches, see our page Three Ways of Expressing Roof Slope.

That page also explains the math that allows you to convert any roof slope expressed in any way to any other way. Pitch to degrees, percentage to degrees, degrees to percentage, etc. This will help you find the conversion equivalent for any slope not listed.

Conversion Formula for Standard Roof Pitch to Degrees

This is how you convert a slope expressed in standard roof pitch (even a slope that include a fraction) to degrees:

1. To convert a roof slope expressed as “X-in-12″ to a roof slope expressed in degrees, find the arctangent of (rise/run).
2. Divide the rise (that’s the “X”, your “X” will vary according to how steep the roof is) by the run (the run is always 12).
3. Using a scientific calculator, find the arctangent of the result.

There’s a good calculator here at web2.0calc.com. Click the “2nd” button (top left of the calculator field). The “atan” (arctangent) button is the second from the bottom on the left side of the calculator field.

First enter the number you got from dividing your rise by your run (0.791667 in the following example).

Then click the “atan” button, and then the “=” button. This will give you the arctangent of (rise/run).

Example:

1. For a slope of 9½-in-12
2. Convert to a decimal: 9½ becomes 9.5
3. Divide 9.5 by 12 (rise/run is 9.5/12) to get 0.791667
4. Find the arctangent of 0.791667
5. Arctan(0.791667) = 38.367497125297
6. Round this to a reasonable number of digits. Let’s call it 38.37.
7. A 9½-in-12 roof slope is the same as a 38.37 degree slope.

Table 1: Standard Roof Pitch to Degrees Conversion

How to Convert Roof Angle in Degrees to Standard Roof Pitch

About This Degrees to Roof Pitch Conversion Table

The following table shows the roof pitch (rise-in-run) equivalents for all roof slopes in degrees from 1° to 72°. Other than the 45° roof slope, which is 12-in-12, none of the standard roof pitches (5-in-12, 6-in-12, etc.) are equal to a whole degree.

To see what the degree or percentage equivalents are for standard rise-in-run roof pitches, see our page Three Ways of Expressing Roof Slope. That page also explains the math that allows you to do the conversions yourself for any slope not listed.

Conversion Formula for Degrees to Standard Roof Pitch

This is how you convert a slope expressed in degrees (even a slope that include a fraction of a degree) to standard roof pitch:

1. Find the tangent of the degree value.
2. Multiply the tangent by the run (which is by convention always 12).
3. That gives you the rise. Put them together as Rise-in-Run.

You can find a good calculator here at web2.0calc.com.

Example:

For a slope of 35.5°:

• tan(35.5) = 0.713
• 0.713 x 12 = 8.556
• giving you a slope of 8.556-in-12 or approximately 8-9/16 in 12.

Table 2: Slopes in Degrees Converted to Standard Roof Pitch

If you’re not sure what the slope of your roof is and you want to determine that in either degrees or rise-in-run, we recommend this slope finder on Amazon. It’s very inexpensive and very accurate.

If you’re using this table, you may want to look into getting yourself a construction calculator. This one is very good.

---

About the Author

---

Related Pages

• How to Find the Area of a Roof
• Minimum Required Roof Pitch for Every Roofing Material
• Roof Pitch Multiplier Table – Roof Pitch Factor Explained
• Roof Slope Equivalents